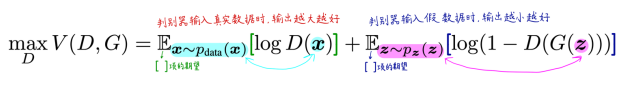GAN开山之作论文解读及感想
研一生涯快结束了,看了一些论文,最终还是决定继续深度学习,本科阶段学过了TensorFlow,也还算有一些基础吧,了解了一下GAN生成对抗网络,写一写学习心得
GAN模型介绍
《Generative Adversarial Nets》是Ian J.Goodfellow发表在NIPS 2014上的一篇
在原文中使用了印假钞的犯罪分子与辨识假钞的警察为例,犯罪分子希望能够印刷骗过警察的假钞,而警察希望能够辨识出假钞。在一次次的博弈中,警察的辨识手段越来越丰富,而犯罪分子的技术也越来越高明。最后,假钞能
这里我想补充一点的是,在警察和印假钞的犯罪分子的博弈之间,警察是需要分辨真钞和假钞的,也就是说,真钞和假钞都是警察所要判断的数据集,而犯罪分子是需要通过自己的手段去使假币尽量成真,也就是说生成器并不是以真实图像作为自己的目标,而是以判别器为目标,生成能够骗过判别器的数据,从而使判别器无法分辨此时的图像是真实的还是
模型结构
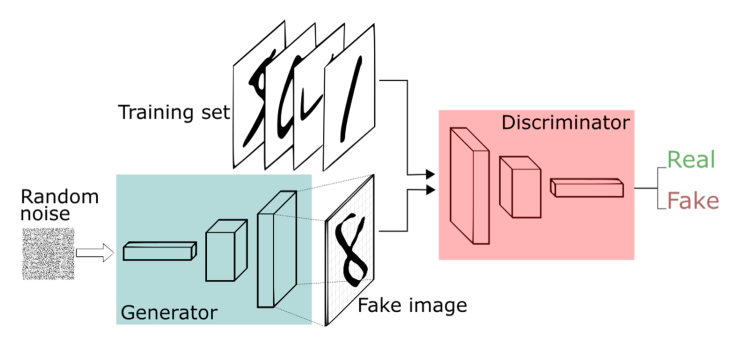
这张图可以简化成下图:
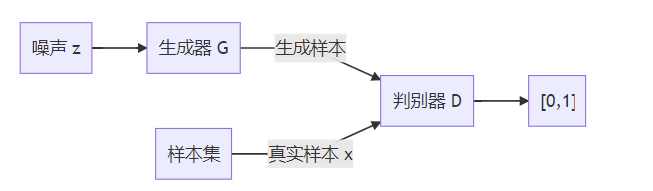
模型分为生成器G和判别器D两部分,生成器G输入噪声z生成样本,判别器D输入真实样x和G生成的样本G(z),并输出表示输入的样本是否为真实样本概率的一个标量。
D希望最大化甄别真实样本的概率
![]()
和甄别生成样本的概率
![]()
而G的目标则是最小化第二项。文中使用V (G ,D)来表述这一过程:

其中,z表示随机噪声,pz(z)表示随机噪声z服从的概率分布,G(z)表示生成器输入z输出假图像,x~p_data表示真实数据服从的概率分布,D(x)表示输入图像输出改图像来自x的概率。
训练过程
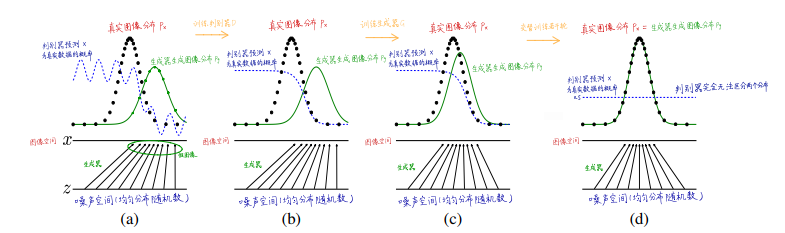
图中黑色虚线表示真实数据分布,蓝色虚线表示判别器预测x为真实数据的概率,绿色实线为生成器生成图像分布,水平线x是图像空间,z为噪声空间。
首先,通过训练判别器D,可以在b图中看出,判别器在前期准确判断的判断率很高,在绿色实线附近蓝色虚线是很低的,这说明在训练刚开始时D能轻易分辨出真实样本,其次,训练生成器G,固定判别器D,此时c图反映出判别器还是能够大概率分辨出真实样本和生成样本,最后,随着生成器和判别器交替训练若干轮,两者达到纳什均衡,此时判别器判断输入是数据是真实数据的概率为0.5,即判别器完全无法区分两个分布。
证明过程
对于给定G,D的最优解为
![]()
由(1)式最大化判别器价值函数
将上式的期望改为积分形式,可以得到:
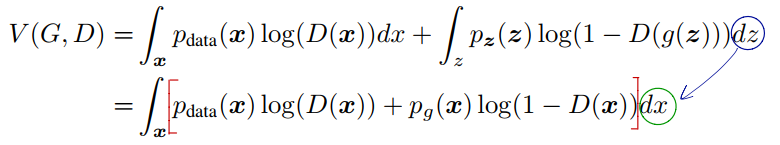
期望与积分的转化其实就是期望的定义:
![]()
而当z-x为单射时,对噪声z采样相当于对假图像采样,故
&nbs![]()
对于任何
![]()
方程
![]()
总是能够在
![]()
时取到最大值,
![]()
在原式中
![]()
因此求得
![]()
这里其实用得是凸函数的性质,推断公式如下:

当且仅当
![]()
时,生成器价值函数C(G)取得全局最小解-log4.


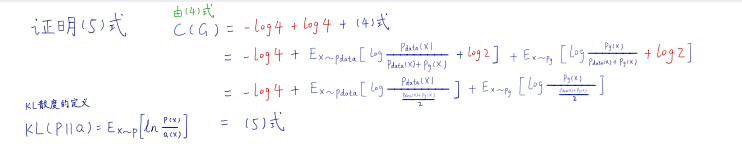
其实此篇文章最难懂的就是数学证明这一部分,这一部分的证明当时也是看的头很大,然后去B站搜了一些视频看,好在最后看懂了一些,GAN的学习之旅算是开了个头,以后要继续深入学习,争取有时间就把感想写下来,把输入转变为输出,继续努力!
本文所提到的文献地址:https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf
最后,书读百遍,其义