L1范数和L2 范数

理解L1，L2 范数

什么是范数ghgfhjfwenzhanglaixzizhenggegedboke@@@@？

在线性代数以及一些数学领域中，norm 的定义是

a function that assigns a strictly positive length or size to each vector in a vector space， except for the zero vector. ——Wikipedia

简单点说，一个向量的 norm 就是将该向量投影到 [0, ) 范围内的值，其中 0 值只有零向量的 norm 取到。

百度百科的解释是：在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。

看到这样的一个范围或者说长度，相信大家就能想到其与现实中距离的类比，于是在机器学习中 norm 也就总被拿来表示距离关系：根据怎样怎样的范数，这两个向量有多远。

上面这个“怎样怎样”也就是范数种类，通常我们称为p-norm，严格定义是：
若

$x=[x_1,x_2,x_3,...,x_n]^T，$

那么

$||x||_p =(|x_1|^p+|x_2|^p+...+|x_n|^p)^{1/p}$

其中当 p 取 1 时被称为 1-norm，也就是提到的 L1-norm，同理 L2-norm 可得。

L2展开就是熟悉的欧ghgfhjfwenzhanglaixzizhenggegedboke@@@@几里得范数：

$||x||_2 = \sqrt{x_1^2+...+x_n^2}$

前面所说的范数啊距离啊基本都是一个变量，对于一些常见的距离这里就可以很简单的说明一下了

理解了什么是范数，现在可以看看L1和L2范数具体的应用了

L1和L2范数在机器学习上最主要的应用大概分为两类：

作为损失函数使用
作为正则项使用

损失函数

1. L1损失函数

L1损失函数也被称为最小绝对值偏差（LAD,least absolute deviation），绝对值损失函数（LAE）。In a word，它是把目标值ghgfhjfwenzhanglaixzizhenggegedboke@@@@y与估计值f(x)的绝对差值的总和最小化.

$L = \sum_{i = 0}^{n}|y_i - f(x_i)|$

2. L2损失函数

L2损失函数也被称为最小平方误差（least squares error,LSE）,或者说是最小二乘误差，它是把目标值y与估计值f(x)的差值的平方和最小化，一般回归问题会使用此损失，离群点对此损失的影响较大

$L = \sum_{i = 0}^{n}|y_i - f(x_i)|^2$

3.二者对比

对于 L1 和 L2 损失函数的选择，大家一般用 L2 损失函数而不用 L1 损失函数的原因就是：计算方便！可以直接求导获得取最小值时各个参数的取值。

此外还有一点，用 L2 一定只有一条最好的预测线，L1 则因为其性质可能存在多个最优解。

当然 L1 损失函数相比于L2损失函数鲁棒性 (Robust) 更强，对异常值更不敏感。

正则化

因为机器学习中众所周知的过拟合问题，所以用正则化防止过拟合，成了机器学习中一个非常重要的技巧。

但数学上来讲，其实就是在损失函数中加个正则项（Regularization Term），ghgfhjfwenzhanglaixzizhenggegedboke@@@@来防止参数拟合得过好。

1. L1正则

L1正则常被用来进行特征选择，主要原因在于L1正则化会使得较多的参数为0，从而产生稀疏解，我们可以将0对应的特征遗弃，进而用来选择特征。一定程度上L1正则也可以防止模型过拟合。

假设 L(W) 是未加正则项的损失，λ是一个超参，控制正则化项的大小。

对应的损失函数：

$L=L(W)+\lambda\sum_{i = 1}^{n}|w_i|$

2. L2正则

L2正则主要用来防止模型过拟合，直观上理解就是L2正则化是对于大数值的权重ghgfhjfwenzhanglaixzizhenggegedboke@@@@向量进行严厉惩罚。鼓励参数是较小值，如果 w 小于1，那么 w^2 会更小。

对应的损失函数：

$L=L(W)+\lambda\sum_{i=1}^{n}(w_i)^2$

3.两者对比

这两个正则项最主要的不同，包括两点：

如上面提到的，L2 计算起来更方便，而 L1 在特别是非稀疏向量上的计算效率就很低；
还有就是 L1 最重要的一个特点，输出稀疏，会把不重要的特征直接置零，而 L2 则不会；
最后，L2 有唯一解，而 L1 不是。

这里关于第二条输出稀疏，为什么 L1 会有这样的性质呢，而 L2 没有呢？这里用个直观的例子来讲解。

首先获知用梯度下降法来优化时，需要求导获得梯度，然后用以更新参数。

那么这里就分别先对 L1 正则项和 L2 正则项来进行求导，可得：

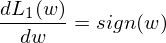
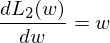
之后画出的L1和L2以及导数图像如下：

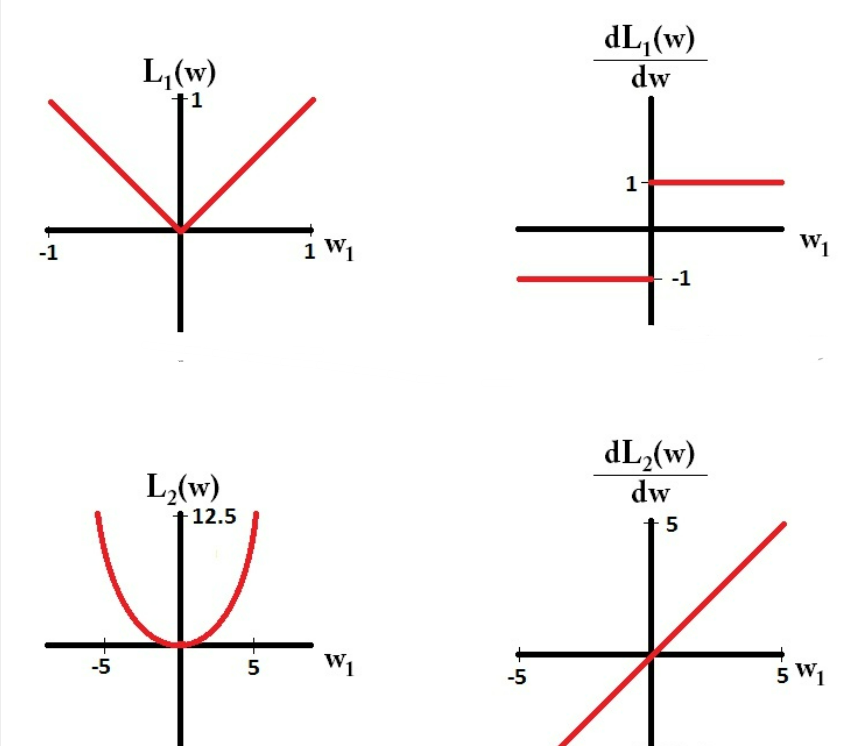
根据图像可以发现，在梯度更新时，不管L1的大小是多少（只要不是0）的梯度都是1或者-1，所以每次更新时，它都是稳步向0前进。

而L2就不同，你会发现它的梯度越靠近0，就变得越小。也就是说加了 L1 正则的话基本上经过一定步数后很可能变为0，而 L2 几乎不可能，因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。