差分隐私–拉普拉斯机制代码实现

差分隐私--拉普拉斯机制代码实现

差分隐私的定义和理解可查看之前所写博客：差分隐私

本文所用数据集在之前所写文章：差分攻击-去标识化代码实现

参考论文：
Smooth sensitivity and sampling in private data analysis

差分隐私是算法的属性，而不是数据的属性。

也就是说，我们可以证明算法满足差分隐私。

为了证明数据集满足差分隐私，我们必须证明产生它的算法满足差分隐私。

定义中的参数称为隐私参数或隐私预算，当的值较小时，要求随机函数F在给定相似的输入时提供非常相似的输出，因此提供更高级别的隐私；当的值较大时，允许输出的相似性降低，因此提供的隐私较少。

普遍的共识是应该在1左右或更小，并且的值高于10可能对保护隐私没有多大作用 ，但这个经验法则可能会变得非常保守。

拉普拉斯机制（The Laplace Mechanism）

差分隐私通常用于回答特定查询，这里还是使用之前用过的人口普查数据作为例子进行操作，查询“数据集中有多少人是40岁以上？”

实现此查询的差分隐私的最简单方法是在其答案中添加随机噪声。关键的挑战是添加足够的噪声来满足差分隐私的定义，但又不能过多地使答案变得过于嘈杂而无用。

为了使这个过程更容易，在差分隐私领域已经开发了一些基本机制，这些机制准确地描述了使用哪种噪声以及使用多少噪声，其中之一就是本文所要提到的拉普拉斯机制。

函数f的灵敏度是当其输入变化1时，f的输出变化量。灵敏度是一个复杂的话题，也是设计差分隐私算法的一个组成部分。现在我们先只支出计数查询的敏感性始终为1，本文最后再来讲讲灵敏度等其他知识。

我们通过使用灵敏度为 1 的拉普拉斯机制和我们选择的来实现示例查询的差分隐私，现在，让我们选择 = 0.1 。我们可以使用Numpy的从拉普拉斯分布中采样。

sensitivity = 1
epsilon = 0.1

adult[adult['Age'] >= 40].shape[0] + np.random.laplace(loc=0, scale=sensitivghgfhjfwenzhanglaixzizhenggegedboke@@@@ity/epsilon)

可以通过多次运行此代码来查看噪声的影响。

每次，输出都会发生变化，但大多数时候，答案与真实答案14235足够接近，因此很有用

噪声多少是足够的？

那么另一个问题来了~

我们怎么知道拉普拉斯机制增加了足够的噪声来防止数据集中个体的重新识别？

让我们先试试一个恶意计数查询，该查询专门用于确定Karrie Trusslove的收入是否大于5万美元。

karries_row = adult[adult['Name'] == ghgfhjfwenzhanglaixzizhenggegedboke@@@@'Karrie Trusslove']
karries_row[karries_row['Target'] == '<=50K'].shape[0]

这个结果肯定侵犯了Karrie的隐私，因为它揭示了Karrie行的收入列的价值。

这时候我们就可以使用拉普拉斯机制确保对查询进行计数的差分隐私，因此我们可以对查询执行以下操作：

sensitivity = 1
epsilon = 0.1

karries_row = adult[adult['Name'] == 'Karrie Trusslove']
karries_row[karries_row['Target'] == '<=50K'].shape[0] + \
  np.random.laplace(loc=0, scale=sensitivity/epsilon)

我跑的第一次，直接是负数了，再跑一次试试

第二次结果还算正常

第三次比较接近1，但还是负数，不断运行这串代码，就可以得到不同的答案，真正的答案是0还是1？噪声太大，无法可靠的分辨出来

这就是差分隐私的工作方式，该方法不会拒绝被确定为恶意的查询，相反，它增加了足够的噪声恶意查询的结果对对手毫无用处。

示例讲完之后，我们再来说说前面所讲的灵敏度，也可称之为敏感度，这是差分隐私的重中之重，接下来我们详细说明。

全局敏感度

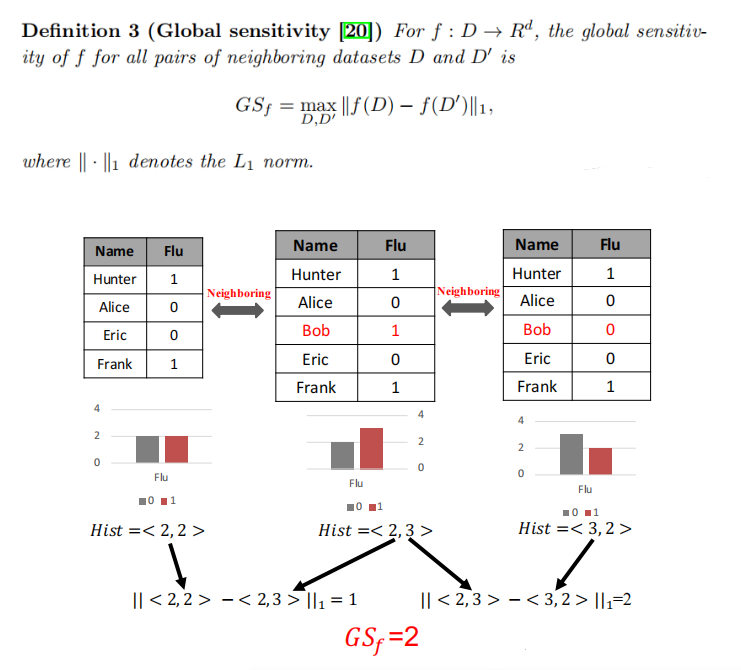
这是论文中对于全局敏感度的定义，我们可以看出，全局敏感度度量在修改一个元组时查询结果的最大变化。它只与查询函数相关，并且独立于数据集本身，对于一些函数，例如和、计数和最大值，全局敏感度很容易计算。例如，计数的全局敏感性为1，因为对于任何两个相邻的数据集，只有一个元组被更改，而对于直方图查询的全局敏感性为2。对于其他一些函数，如计算kmeans簇的最大直径和计数子图，全局灵敏度可能难以计算或无界。

对于全局灵敏度较小的函数，只需要添加少量的噪声，以掩盖在更改一条记录时对查询结果的影响。然而，当全局灵敏度较大时，需要向输出添加大量的噪声，以确保隐私保证，从而导致数据效用较差。针对不同的问题，提出了两种噪声机制，即拉普拉斯机制和指数机制。

局部敏感度

当全局灵敏度较大时，必须向输出中添加大量的噪声，以实现差分隐私，这可能会严重损害数据效用。为了解决这个问题，Nissim等人提出了局部灵敏度的思想

局部敏感度不仅与查询函数f有关，而且还与给定的数据集d有关。根据定义3，GSf=maxD(LSf(D))。由于噪声的大小与灵敏度成正比，噪声的局部灵敏度要小得多。不幸的是，局部灵敏度不能满足差分隐私的要求，因为噪声大小本身可能会揭示数据库信息。例如，考虑一个数据库，其中的值在0和M>0之间，以及两个相邻的数据库D(0、0、0、0、0、M、M)和D0(0、0、0、0、M、M、M)。设f为中值函数。然后，f(D)=0和f(D0)=0，以及相应的局部灵敏度为LSf(D)=0和LSf(D0)=M。相应地，如果噪声分别根据0和M进行校准，以计算A(D)和A(D0)，那么它们很容易被对手区分。如果采用局部灵敏度，算法A不是（，）差异私有的。为了弥合差距，提出了一个局部灵敏度的光滑上界来确定所添加的噪声的大小。

平滑敏感度

当=0，S(D)成为常数GSf，以满足定义5中的要求。全局灵敏度是LSf上一个简单但可能松散的上界。当>0时，全局灵敏度是LSf的一个保守上界。LSf可能有多个平滑边界，并且平滑灵敏度是符合定义5的最小边界。

当光滑灵敏度难以计算时，就使用光滑上界来代替光滑灵敏度。接下来，我们将展示如何使用平滑灵敏度（或上界）来校准-差异隐私的噪声。对数据集D上的查询f返回A(Dghgfhjfwenzhanglaixzizhenggegedboke@@@@)=f(D)+Z，其中Z是从一个分布中抽取的随机变量。如果Z∼Lap(GSf/)，A(D)提供了-的差异隐私。在-的差异隐私中，添加的噪声的大小应该尽可能小，以保持数据效用，并且应该独立于数据ghgfhjfwenzhanglaixzizhenggegedboke@@@@库，以进行强大的隐私保护。根据全局灵敏度校准的噪声独立于数据库D，但其大小可能太大，无法使查询结果不可用。根据局部灵敏度校准的噪声依赖于D，使其失效，导致差异隐私。为了解决这个挑战，Nissim等人。建议使用根据局部灵敏度的平滑上界（更优选的是平滑灵敏度）进行校准的噪声。其基本思想是添加与Sf(D)成正比的噪声，即A(D)=f(D)+Sf(D)Z，其中Sf是f局部灵敏度的平滑上界，Z是一个具有概率密度函数h的随机变量。Nissim等人指出，h必须允许（，），以实现基于平滑灵敏度的差异隐私。

思考

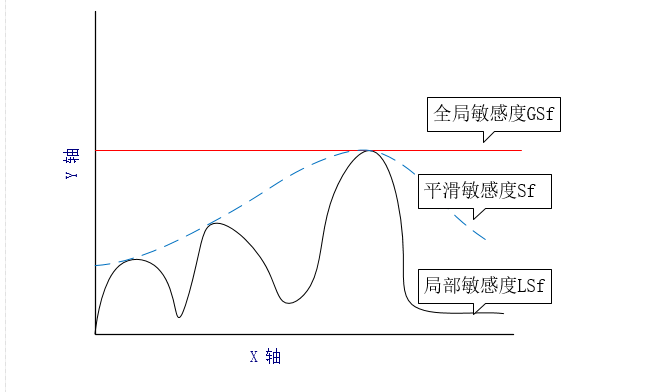
全局敏感度：考虑最极端的情况，不管你的数据怎么分布，只看查询。我把它想象成数学概念中的函数最大值。

局部敏感度：查询也看，数据也看。从形式化定义来看，局部敏感度是依赖于给定的数据集的，在给定的数据集中变一条记录找最大影响，这个影响大小就是局部敏感度。我把它想象成数学概念中的函数极大值，这么理解是不是就能很好的区分出全局敏感度和局部敏感度了？看上去好像完美无缺，实际已经都不能算差分隐私了。为什么？因为数据集不可能永远不变，每次改变，局部敏感度是不是要变，那么是不是体现出了数据分布的差异。

平滑敏感度：找到一个平滑上界函数，不同的函数会导致上界不同。全局敏感度作为局部敏感度较为松弛的上界，平滑敏感度是较为保守的上界。平滑上界考虑的是改变多条记录的最大敏感度，再乘以一个平滑上界函数，这个函数的目的在于做一个惩罚，这个函数一定小于1。